1. Stany koherentne
Widzieliśmy, że wartość średnia amplitudy pola jest równa zeru dla stanu \(n\) fotonowego. Z drugiej strony, wiemy, że klasyczna amplituda światła drga harmonicznie. Oznacza, to, że stany Focka są silnie nieklasyczne, nie można ich obecności zaobserwować w eksperymencie w warunkach klasycznych. Możemy zastanawiać się, czy istnieją może takie stany kwantowe, które w lepszym stopniu odpowiadają klasycznemu scenariuszowi.
Okazuje się, że stanami takimi są stany własne operatora anihilacji, co pokażemy w dalszej części. Rozważmy stany własne operatora \(a\), które oznaczymy jako \(|{\alpha}\rangle\).
\begin{equation}
a|{\alpha}\rangle = \alpha |{\alpha}\rangle
\tag{1}
\end{equation}
Ponieważ stany Focka tworzą bazę, to możemy rozwinąć stany \(|{\alpha}\rangle\) w tej bazie:
\begin{equation}
|{\alpha}\rangle = \sum_{n = 0}^{+\infty} A_{n}|{n}\rangle
\tag{2}
\end{equation}
Podstawiając do równania własnego, dostajemy:
\begin{equation}
a |{\alpha}\rangle = \sum_{n = 1}^{+\infty} A_{n}\sqrt{n}|{n-1}\rangle = \alpha\sum_{n=0}^{+\infty}A_{n}|{n}\rangle
\tag{3}
\end{equation}
Dostajemy w efekcie stosunek kolejnych sąsiadów w ciągu amplitud:
\begin{equation}
\frac{\alpha}{\sqrt{n}} = \frac{A_{n}}{ A_{n-1}}
\tag{4}
\end{equation}
co daje nam rozwiązanie jako:
\begin{equation}
A_{n} = A_{0}\frac{\alpha ^{n}}{\sqrt{n!}}
\tag{5}
\end{equation}
Stany powinny być unormowane do \(1\) aby reprezentowały dobrze zdefiniowane stany kwantowe:
\[
\langle \alpha | \alpha \rangle = 1 = |A_0|^{2} \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \frac{(\alpha^{*})^{m} \alpha^{n}}{\sqrt{m! \, n!}} \langle m | n \rangle = |A_0|^{2} e^{|\alpha|^{2}} \tag{6}
\]
gdzie wykorzystaliśmy rozwinięcie funkcji \(\exp\) w szereg potęgowy.
Ponieważ faza względna może zostać zawsze wyeliminowana, to \(A_{0}\) możemy przyjąć jako rzeczywiste. Wtedy:
\begin{equation}
A_{0} = e^{-|\alpha|^{2}/2}
\tag{7}
\end{equation}
Stan koherentny przyjmuje zatem postać w bazie Focka:
\begin{equation}
|{\alpha}\rangle = e^{-|\alpha|^{2}/2}\sum_{n=0}^{+\infty}\frac{\alpha^{n}}{\sqrt{n!}}|{n}\rangle
\tag{8}
\end{equation}
Zauważmy, że nigdzie w tym rozumowaniu nie założyliśmy nic o postaci liczby \(\alpha\). Wynika stąd, że wartości własne operatora kreacji pokrywają całą płaszczyznę zespoloną.
Zauważmy, że różne stany koherentne, nie są ortogonalne. Dla dwóch różnych stanów koherentnych, danych przez liczby zespolone \(\beta\) oraz \(\alpha\), zachodzi:
\[
\langle \beta | \alpha \rangle = e^{-\frac{|\alpha|^{2} + |\beta|^{2}}{2}} \sum_{n=0}^{\infty} \sum_{m=0}^{\infty} \frac{(\beta^{*})^{n} \alpha^{m}}{\sqrt{n! \, m!}} \langle n | m \rangle = e^{-\frac{|\alpha|^{2} + |\beta|^{2}}{2}} e^{\beta^{*} \alpha} \tag{9}
\]
Rozważmy kwadrat modułu przekrycia tych stanów:
\[
|\langle \beta | \alpha \rangle|^{2} = e^{-|\alpha|^{2} + |\beta|^{2}} e^{2 \operatorname{Re}[\beta^{*} \alpha]} = e^{-|\alpha|^{2} + |\beta|^{2}} e^{\beta^{*} \alpha + \alpha^{*} \beta} = e^{-|\alpha – \beta|^{2}} \tag{10}
\]
Kwadrat modułu iloczynu skalarnego zanika eksponencjalnie wraz ze wzrostem odległości między tymi dwoma punktami. Stany bardzo odległe, stają się więc prawie ortonormalne.
W związku z powyższym, nasuwa się nam zasadnicze pytanie. Czy stany koherentne tworzą bazę w przestrzeni Hilberta? Okazuje się, że nie. Co prawda, stany koherentne są zbiorem rozpinającym przestrzeń Hilberta, natomiast nie są one liniowo niezależne, zatem nie spełniają warunków bazy. Mówimy że układ taki jest nadzupełny. Stany koherentne spełniają natomiast inną ciekawą zależność: można utworzyć z nich operator identyczności na wzór operatora identyczności tworzonego z wektorów bazy zupełnej i ortonoramalnej. Spełniona jest równość:
\[
I = \frac{1}{\pi} \int_{\mathbb{C}^{2}} d^{2}\alpha \, | \alpha \rangle \langle \alpha | \tag{11}
\]
Ścisły dowód matematyczny tej zależności jest wymagający i nie wnosi nic istotnego do treści naszego kursu, dlatego pozostawimy tę zależność bez dowodu.
Jesteśmy teraz przygotowani do tego, żeby policzyć kluczowe wielkości związane z polem kwantowych w stanie koherentnym.
Zacznijmy od wartości średniej operatora \(Q\), który jest proporcjonalny do operatora pola elektrycznego. Ponieważ \(a|{\alpha}\rangle = \alpha|{\alpha}\rangle\) oraz \(\langle \alpha | a^{\dagger} = \langle \alpha | \alpha^{*} \):
\[
\langle \alpha | Q | \alpha \rangle = \frac{1}{2} \left( \alpha e^{-i\omega t} + \alpha^{*} e^{i\omega t} \right) = \operatorname{Re} \left[ \alpha e^{-i\omega t} \right] \tag{12}
\]
Tak samo dla operatora pędu:
\[
\langle \alpha | P | \alpha \rangle = \frac{1}{2i} \left( \alpha e^{-i\omega t} – \alpha^{*} e^{i\omega t} \right) = \operatorname{Im} \left[ \alpha e^{-i\omega t} \right] \tag{13}
\]
Obliczmy teraz średnią kwadratów tych operatorów:
\[
\langle \alpha | Q^{2} | \alpha \rangle = \frac{1}{4} \left( \alpha^{2} e^{-i 2 \omega t} + (\alpha^{*})^{2} e^{i 2 \omega t} + 2 |\alpha|^{2} + 1 \right) \tag{14}
\]
\[
\langle \alpha | P^{2} | \alpha \rangle = \frac{-1}{4} \left( \alpha^{2} e^{-i 2 \omega t} + (\alpha^{*})^{2} e^{i 2 \omega t} – 2 |\alpha|^{2} – 1 \right) \tag{15}
\]
Podstawiając obliczone wartości otrzymujemy nieoznaczoność obu operatorów w stanie koherentnym:
\begin{equation}
\sigma_{Q} = \sigma_{P} = \frac{1}{2}
\tag{16}
\end{equation}
Otrzymany wynik możemy podsumować istotnym stwierdzeniem: Stany koherentne minimalizują zasadę nieoznaczoności operatorów pędu i położenia kanonicznego, czyli operatorów pola elektrycznego i magnetycznego. Jest to wynik, który pozwala nam je traktować jako przynależne do grupy najbardziej klasycznych spośród stanów kwantowych pola.
Otrzymane rezultaty są jeszcze ciekawsze, jeżeli zauważymy, że względem wartości średniej, część zespolona liczby \(\alpha\) odpowiada pędowi, a część rzeczywista odpowiada położeniu. Możemy zatem liczbę \(\alpha\) interpretować jako zespolony opis przestrzeni fazowej oscylatora harmonicznego. Ze względu na omawianych kwantowość zjawisk, przestrzeń fazowa (czyli w fizyce klasycznej przestrzeń położeń i pędów) określa nie konkretne stany, położeń i pędów ale grupy stanów koherentnych znajdujących się w obszarze o środku w punkcie \(\alpha\) oraz o szerokości \(1/2\) wyznaczonej przez odchylenie standardowe wyników.
Rysunek 2. Reprezentacja stanu koherentnego w przestrzeni fazowej.
Jeżeli zapiszemy charakterystykę stanu koherentnego w postaci biegunowej : \(\alpha = |\alpha|e^{i\phi}\), to średnia operatora pola elektrycznego odpowiada po prostu profilowi klasycznej fali stojącej:
\[
\langle \alpha | E_{x}(x,t) | \alpha \rangle = |\alpha| \, \mathcal{E}_{0} \cos(\omega t + \phi) \sin(k z) \tag{17}
\]
natomiast moduł \(\alpha\), jest odpowiedzialny za modulację amplitudy tej fali.
Zgodnie z naszymi wcześniejszymi ustaleniami, ze względu na to, iż moduł \(\alpha\) oraz amplituda pola elektrycznego są ze sobą związane, to moglibyśmy podejrzewać, że im wyższa wartość modułu \(\alpha\), tym bardziej klasyczny stan powinniśmy otrzymywać. Z drugiej strony, intuicja podpowiada nam, iż ze względu na to iż rejestrowanie pojedynczych fotonów w klasycznym eksperymencie nie jest możliwe, to stany „najbardziej klasyczne” powinny posiadać dużą liczbę fotonów.
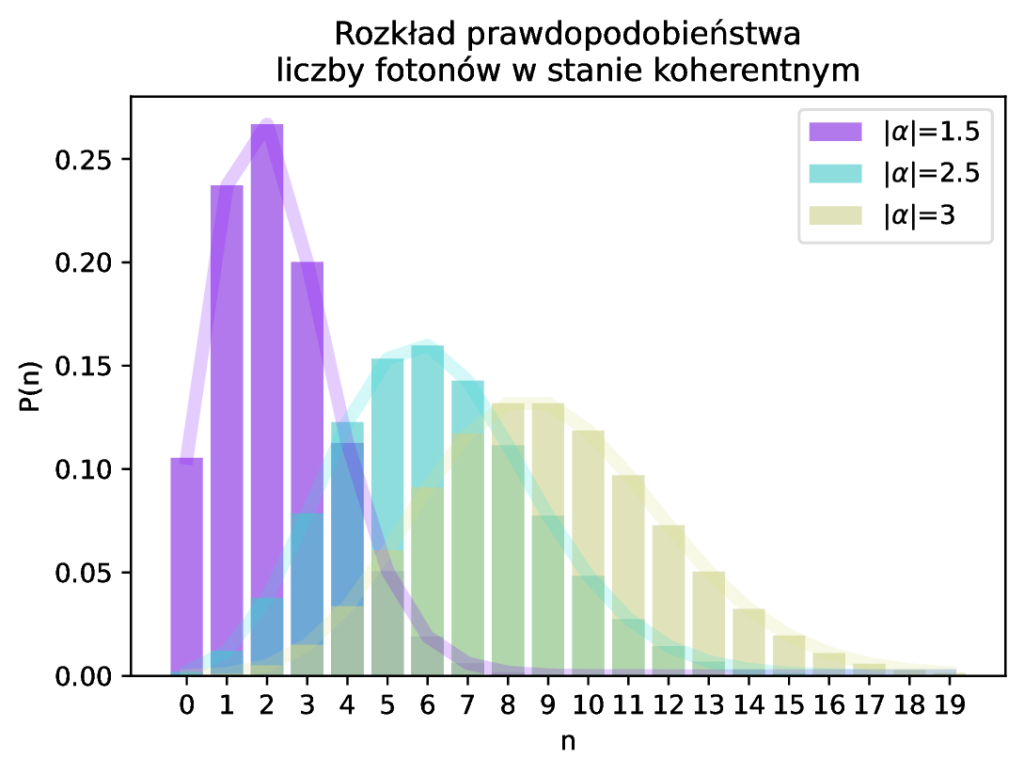
Aby się przekonać czy tak w rzeczywistości jest, obliczmy statystykę liczby fotonów w stanie koherentnym. Prawdopodobieństwo tego, że w stanie koherentnym pola \(|{\alpha}\rangle\) znajdziemy \(n\) fotonów jest dane przez kwadrat modułu amplitudy prawdopodobieństwa:
\[
P(n) = |\langle n | \alpha \rangle|^{2} = e^{-|\alpha|^{2}} \left| \sum_{m=0}^{\infty} \frac{\alpha^{m}}{\sqrt{m!}} \langle n | m \rangle \right|^{2} = \frac{|\alpha|^{2n}}{n!} e^{-|\alpha|^{2}} \tag{18}
\]
Przypomnijmy, że rozkład Poissona zmiennej dyskretnej o wartościach \(n\) i wartości oczekiwanej \(\lambda\), jest dany równaniem
\begin{equation}
P(n) = \frac{\lambda^{n}}{n!}e^{-\lambda}
\tag{19}
\end{equation}
Z własności rozkładu Poissona, otrzymany wynik daje nam od razu dwa ciekawe wnioski. Pierwszy z nich mówi nam, że średnia liczba fotonów w stanie koherentnym jest dokładnie równa kwadratowi modułu liczby \(\alpha\):
\begin{equation}
\langle n\rangle = |\alpha|^{2}
\tag{20}
\end{equation}
Drugi, mówi nam, że nieoznaczoność liczby fotonów w stanie koherentnym, jest równa modułowi \(\alpha\):
\begin{equation}
\sigma_{n} = |\alpha|
\tag{21}
\end{equation}
Zatem, im większy jest moduł liczby \(\alpha\), tym większa staje się oczekiwana liczba fotonów oraz tym mniej pewni jesteśmy jej dokładnej liczby. Takie ustalenia potwierdzają naszą wcześniejszą intuicję, a mianowicie, że stany koherentne pola kwantowego, o dużej amplitudzie \(|\alpha|\) są najbliżej spokrewnione z klasycznymi stanami pola elektromagnetycznego, w którym liczba fotonów jest tak duża i na tyle rozmyta, że ich kwantowa natura staje się niezauważalna.
Na koniec, rozważań, wykreślmy jeszcze rozkład prawdopodobieństwa liczby fotonów, dla różnych amplitud stanu koherentnego.
import numpy as np import matplotlib.pyplot as plt from matplotlib import cm import seaborn as sns # amplitudy stanów koherentnych amps = [1.5, 2.5, 3] P_n = lambda a, n : np.exp(-a**2) * (a**2)**n / np.vectorize(np.math.factorial)(n) n = np.arange(0, 20) fig = plt.figure(figsize = (6,4)) ax = fig.add_subplot(1, 1, 1) for i, a in enumerate(amps): P = P_n(a, n) sns.barplot( x = n,y = P, label= (r"$|\alpha|$" + f"={a}"), color=cm.rainbow(i / len(amps)), ax = ax, alpha = 0.6) sns.lineplot( x = n, y = P, color=cm.rainbow(i / len(amps)), ax = ax, alpha = 0.2, lw = 5) ax.set_title("Rozkład prawdopodobieństwa\nliczby fotonów w stanie koherentnym") ax.set_xlabel("n") ax.set_ylabel("P(n)") ax.legend(loc="upper right") plt.show()